RCWA法はざっくりいうと、
1.各層の電場をフーリエ級数展開で設定し、
2.境界条件によって展開係数を解いて行く
方法です。
何回かに分けて、RCWA法についてまとめていきます。
今回は「各領域の電場・磁場の式の形を導出する」ところまで行きます。
状況設定
簡単化のために、1次元バイナリ回折格子(長方形凹凸が1層のみ)を考えます。
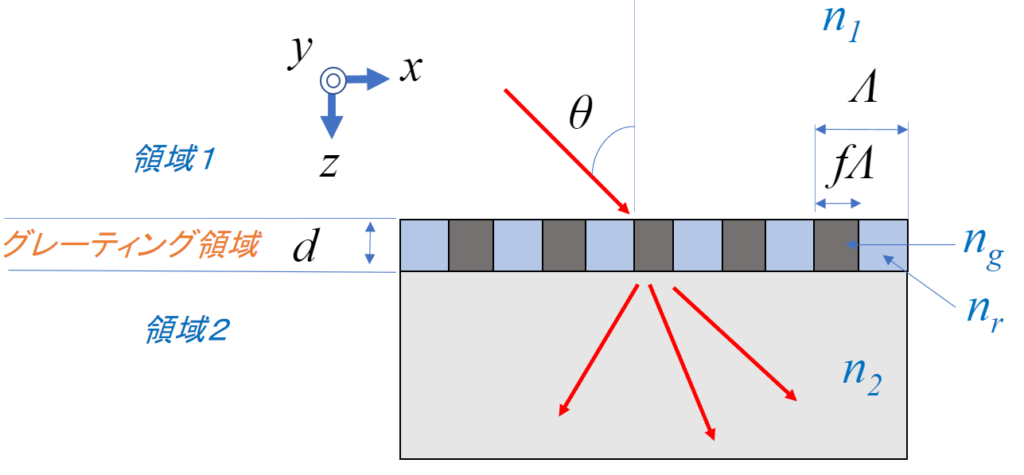
TE波の場合
TE波(transverse electric)とは、入射電場(E)のy成分のみが値を持つ場合です。この場合のみ考えます。
A1. 領域1
TE波の定義から、次のように規格化して表します。
入射波:$$E_{in,y}=\exp(-ik_0n_1(\sin\theta x+\cos\theta z))\tag{A1-1}$$
ここで、時間依存項は\(\exp(+i\omega t)\)とし、省略しています。波数ベクトルが\(\boldsymbol{k_1}=k_0n_1(\sin\theta,0,\cos\theta)\)の平面波を仮定しています。当たり前ですが波数\(k_0\)と波長\(\lambda\)の間に、\(k_0=2\pi/\lambda\)の関係があります。
平面波が回折格子で回折する際、逆格子ベクトル\(2\pi/\Lambda\)の整数倍だけ波数ベクトルのx成分が変化する。\(i\)次の回折光の波数ベクトル\(x\)成分は:
$$k_{xi}=\boldsymbol{k_1}-\frac{2\pi}{\Lambda}i=k_0(n_1\sin\theta-\frac{\lambda_0}{\Lambda} i)\tag{A1-2}$$
で表せる。
波数ベクトルのz成分$k_z$は、マクスウェル方程式から導かれる次の分散関係を満たす。
$$k_{xi}^2+k_{zi}^2=\epsilon\mu\omega^2=(k_0n_l)^2\quad(l=1,2) \tag{A1-3}$$
\(\epsilon,\mu\)は誘電率と透磁率です。つまり、\(k_z\)は:
$$k_{l,zi}=\cases{+k_0\sqrt{n_l^2-(k_{xi}/k_0)^2} & if \(k_0n_l>|k_{xi}|\) \cr -ik_0\sqrt{(k_{xi}/k_0)^2-n_l^2} & if \(k_0n_l<|k_{xi}|\)} \tag{A1-4}$$
となる。\(l=1\)のときは入射領域(領域1)、\(l=2\)のときは出射領域(領域2)を表す。すなわち、\(k_{xi}\)の絶対値が小さい(回折次数が小さい)領域では、波数ベクトルが実数なので回折光が伝搬する。\(k_{xi}\)の絶対値が大きい(回折次数が大きい)領域では、波数ベクトルが虚数となり、指数関数で減衰する波になる。
回折次数\(i\)の振幅反射率\(R_i\)を用いて、入射領域の電場は次で表せる:
$$E_{1,y}=E_{in,y}+\sum_i R_i \exp(-i(k_{xi}x-k_{1,zi}z)) \tag{A1-5}$$
磁場についても考えましょう。マクスウェル方程式\((\nabla\times\boldsymbol{E}=-\partial\boldsymbol{B}/\partial t=-i\omega\mu_0\boldsymbol{H}\))を用います。磁場はx成分、電場はy成分のみであるので、
$$H_x=-\left(\frac{i}{\omega\mu_0}\right)\frac{\partial E_y}{\partial z}=-i\sqrt{\frac{1}{\mu_0}}\frac{1}{k_0}\frac{\partial E_y}{\partial z} \tag{A1-6}$$
となる、これを用いると、
$$H_{in,x}=-i\sqrt{\frac{1}{\mu_0}}(-in_1\cos\theta)\exp(-ik_0n_1(x\sin\theta+z\cos\theta)) \tag{A1-7}$$
$$H_{1,x}=H_{in,x}-i\sqrt{\frac{1}{\mu_0}}\sum_i R_i\frac{ik_{1,zi}}{k_0}\exp(-i(k_{xi}x-k_{1,zi}z)) \tag{A1-8}$$
A2. 領域2
領域1と同様にして、出射領域(領域2)の電場も回折次数で展開して、次のようにかける:
$$E_{2,y}=\sum_iT_i\exp(-i(k_{xi}x+k_{2,zi}(z-d))) \tag{A2-1}$$
\(d\)はグレーティング領域の厚みを示しています。式的には\(z-d\)にする必要はないですが、数値解析時の安定化のためにこのようにしてます。
磁場も領域1と同様にして解けます:
$$H_{2,x}=-i\sqrt{\frac{1}{\mu_0}}\sum_i T_i\frac{-ik_{2,zi}}{k_0}\exp(-i(k_{xi}x+k_{2,zi}(z-d))) \tag{A2-2}$$
A3. グレーティング領域
誘電率分布をフーリエ級数展開する
グレーティング領域は、まず誘電率\(\epsilon\)をフーリエ級数展開します:
$$\epsilon(x)=\sum^{\infty}_{h=-\infty}\epsilon_h\exp(2\pi ihx/\Lambda)\tag{A3-1}$$
フーリエ級数展開の関係式で\(\epsilon_h\)は:
$$\epsilon_h=\frac{1}{\Lambda}\int^{\Lambda/2}_{-\Lambda/2}\epsilon(x)\exp(-2\pi ixh/\Lambda)dx\tag{A3-2}$$
とかける。ここで仮想したバイナリーの場合、簡単にこの積分ができて、
$$\epsilon_h =\cases{(n_r^2-n_g^2)\frac{\sin(\pi hf)}{\pi h} & if \(h\neq 0\) \cr n^2_r+n_g^2(1-f) & if \(h=0\) }\tag{A3-3}$$
が得られます。
電場のモード展開をする
グレーティング領域の電場を表す展開基底(モード)を得るため、電場の\(y\)成分と磁場の\(x\)成分を展開します。
$$E_{g,x}=\sum_i S_{yi}(z)\exp(-ik_{xi}x)\tag{A3-4}$$
$$H_{g,x}=-i\sqrt{\frac{1}{\mu_0}}\sum_i U_{xi}(z)\exp(-ik_{xi}x)\tag{A3-5}$$
\(x\)依存項と\(z\)依存項目をこのようにエイヤと分けます。マクスウェル方程式:
$$\nabla\times \boldsymbol{E}=-\frac{\partial\boldsymbol{B}}{\partial t}\tag{A3-6}$$
$$\nabla\times\boldsymbol{H}=\boldsymbol{J}+\frac{\partial \boldsymbol{D}}{\partial t}\tag{A3-7}$$
と、関係式 \(\boldsymbol{B}=\mu_0\boldsymbol{H},\boldsymbol{D}=\epsilon\boldsymbol{E}\),時間依存性が\(\exp(+i\omega t)\)を用いて、
$$\nabla\times \boldsymbol{E}=-i\omega\mu_0\boldsymbol{H}\tag{A3-8}$$
$$\nabla\times \boldsymbol{H}=i\omega\epsilon(x)\boldsymbol{E}\tag{A3-9}$$
とが得られる。ここで、電流密度は\(\boldsymbol{J}=0\)を仮定しています。電場がy成分しか持たないため、次のように書き換えられる:
$$\frac{\partial E_{g,y}}{\partial z}=i\omega\mu_0H_{g,x}\tag{A3-10}$$
$$\frac{\partial H_{g,x}}{\partial z}=i\omega\epsilon(x)E_{g,y}+\frac{\partial H_{g,z}}{\partial x}\tag{A3-11}$$
先程の級数展開を用いて各\(k_{xi}\)での成分が等しいとすれば、
$$\frac{\partial S_{yi}(z)}{\partial z}=k_0U_{xi}(z)\tag{A3-12}$$
となる。ここで、\(\omega\sqrt{\epsilon_0\mu_0}=\omega/c=k_0\)を使っている。
A3-11式は少し厄介で、A3-10を一度x微分する
$$\frac{\partial H_{g,x}}{\partial x}=\frac{i}{\omega\mu_0}\frac{\partial^2 E_{g,y}}{\partial x^2} \tag{A3-13}$$
これをA3-11式に代入して、
$$\frac{\partial H_{g,x}}{\partial z}=i\omega\epsilon(x)E_{g,y}+\frac{i}{\omega\mu_0}\frac{\partial^2 E_{g,y}}{\partial x^2}\tag{A3-14} $$
となる。Eだけの式になったので、級数展開式を用いて各$k_{xi}$成分を等しいと置くいて解く(ここで\(\epsilon(x)=\sum \epsilon_h\)があることに注意)
$$\frac{\partial U_{xi}(z)}{\partial z}=-k_0\sum_p \epsilon_{i-p}S_{yp}+\left(\frac{k_{xi}^2}{k_0}\right)S_{yi} \tag{A3-15}$$
固有値を解く
A3-12、A3-15を行列表現すると次になる
$$\left(\matrix{\frac{\partial \mathbf{S}_y}{\partial z} \cr \frac{\partial \mathbf{U}_x}{\partial z}}\right)=\left(\matrix{0 & \mathbf{I} \cr \boldsymbol{A} & 0}\right)\left(\matrix{\mathbf{S}_y \cr \mathbf{U}_x}\right) \tag{A3-16}$$
ここで、\(\mathbf{I}\)は単位行列、\(\mathbf{A}=\mathbf{K}_x^2-\mathbf{E}\), \(\mathbf{K}_x\)は\(k_{xi}/k_0\)を成分とする対角行列、\(\mathbf{E}\)は\(\epsilon_{i-p}\)を\(i,p\)成分とする行列です。
更にA3-16を一つの式に直すと、
$$\frac{\partial^2 \mathbf{S}_y}{\partial (z^2)}=\mathbf{AS}_y\tag{A3-17}$$
の形になる。ここまで来ると固有値を用いて書きたくなる
電場の展開係数の$z$依存性を\(\exp(qk_0z)\)と仮定すると、
$$q^2\mathbf{S}_y=\mathbf{AS}_y\tag{A3-18}$$
となる。これは、行列\(\mathbf{A}\)のm番目の固有値\(g_m\)とすると、\(q_m=\pm \sqrt{g_m}\)となる。ここで、固有値\(g_m\)に対する固有ベクトル\(\mathbf{w}_m=(w_{1,m},\;w_{2,m},\;\cdots)\)とすると、グレーティング領域を表す電磁場の固有モードは
$$ E_m =\sum_i w_{i,m}\exp(\pm q_m k_0 z)\exp(-ik_{xi}x)\tag{A3-19}$$
と得られる。行列\(\mathbf{A}\)はエルミート行列であるため(詳細省略…!)、固有値\(q_m\)は必ず実数になり、z方向にはエバネッセント波となっている。
固有モードに対応する磁場は、微分計算で次のように得られる
$$ H_m=-i\left(\frac{1}{\mu_0}\right)^{1/2}\sum_iw_{i,m}(\pm)q_m\exp(\pm q_mk_0z)\exp(-ik_{xi}x)\tag{A3-20}$$
これで\(S_{yi},U_{xi}\)が展開できます。一つの固有値\(q_m\)に対して、z軸の両方向に進む波があるので、異なるモードの重ね合わせを用いると
$$S_{yi}(z)=\sum_{m=1}^nw_{i,m}(c^+_m\exp(-k_0q_mz)+c^-_m\exp(k_0q_m(z-d))\tag{A3-21}$$
$$U_{xi}(z)=\sum_{m=1}^nv_{i,m}(-c^+_m\exp(-k_0q_mz+c^-_m\exp(k_0q_m(z-d)))\tag{A3-22}$$
ここで、\(c^\pm\)は決定すべき未知数で,\(\pm z\)方向に進む波の展開係数です。\(v_{i,m}=w_{i,m}q_m\)で、\(\mathbf{Q}=\left(\matrix{q_1 & & \cr & q_2 & \cr & & \ddots}\right),\mathbf{V}=\left(\matrix{v_1 \cr v_2 \cr \vdots}\right)\)とおくと
$$\mathbf{V}=\mathbf{WQ}\tag{A3-23}$$
とかけます。
A4 小まとめ
各領域の電場・磁場をこれまで式の形にしてきました。これをまとめて書くと次のようになります
領域1(入射領域)
$$E_{1,y}=E_{in,y}+\sum_i R_i \exp(-i(k_{xi}x-k_{1,zi}z))$$
$$E_{in,y}=\exp(-ik_0n_1(\sin\theta x+\cos\theta z))$$
$$H_{in,x}=-i\sqrt{\frac{1}{\mu_0}}(-in_1\cos\theta)\exp(-ik_0n_1(x\sin\theta+z\cos\theta))$$
$$H_{1,x}=H_{in,x}-i\sqrt{\frac{1}{\mu_0}}\sum_i R_i\frac{ik_{1,zi}}{k_0}\exp(-i(k_{xi}x-k_{1,zi}z)) $$
グレーティング領域
$$E_{g,x}=\sum_i S_{yi}(z)\exp(-ik_{xi}x)$$
$$H_{g,x}=-i\sqrt{\frac{1}{\mu_0}}\sum_i U_{xi}(z)\exp(-ik_{xi}x)$$
$$S_{yi}(z)=\sum_{m=1}^nw_{i,m}(c^+_m\exp(-k_0q_mz)+c^-_m\exp(k_0q_m(z-d))$$
$$U_{xi}(z)=\sum_{m=1}^nv_{i,m}(-c^+_m\exp(-k_0q_mz+c^-_m\exp(k_0q_m(z-d)))$$
領域2(出射領域)
$$E_{2,y}=\sum_iT_i\exp(-i(k_{xi}x+k_{2,zi}(z-d)))$$
$$H_{2,x}=-i\sqrt{\frac{1}{\mu_0}}\sum_i T_i\frac{-ik_{2,zi}}{k_0}\exp(-i(k_{xi}x+k_{2,zi}(z-d)))$$
RCWAの目的の一つとして、回折効率(\(R_i,T_i\))を求めていくことにあります。次の記事で行列を解いて、効率を求めていきたいと思います。


コメント