前回の記事で、各領域の電場・磁場の式を立てました。
今回は回折効率を求めていきましょう。
B1.おさらい
状況設定はこの図のようなバイナリ回折格子でした。
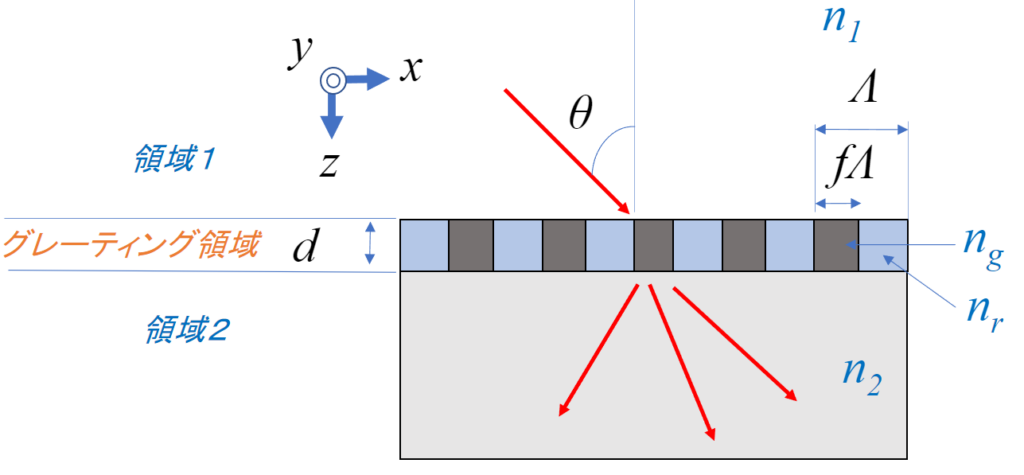
前の記事で求めた式は以下の通り。
領域1(入射領域)
$$E_{1,y}=E_{in,y}+\sum_i R_i \exp(-i(k_{xi}x-k_{1,zi}z)) \tag{B1-1}$$
$$E_{in,y}=\exp(-ik_0n_1(\sin\theta x+\cos\theta z)) \tag{B1-2}$$
$$H_{1,x}=H_{in,x}-i\sqrt{\frac{1}{\mu_0}}\sum_i R_i\frac{ik_{1,zi}}{k_0}\exp(-i(k_{xi}x-k_{1,zi}z)) \tag{B1-3}$$
$$H_{in,x}=-i\sqrt{\frac{1}{\mu_0}}(-in_1\cos\theta)\exp(-ik_0n_1(x\sin\theta+z\cos\theta)) \tag{B1-4}$$
グレーティング領域
$$E_{g,x}=\sum_i S_{yi}(z)\exp(-ik_{xi}x) \tag{B1-5}$$
$$H_{g,x}=-i\sqrt{\frac{1}{\mu_0}}\sum_i U_{xi}(z)\exp(-ik_{xi}x) \tag{B1-6}$$
$$S_{yi}(z)=\sum_{m=1}^nw_{i,m}(c^+_m\exp(-k_0q_mz)+c^-_m\exp(k_0q_m(z-d)) \tag{B1-7}$$
$$U_{xi}(z)=\sum_{m=1}^nv_{i,m}(-c^+_m\exp(-k_0q_mz+c^-_m\exp(k_0q_m(z-d))) \tag{B1-8}$$
領域2(出射領域)
$$E_{2,y}=\sum_iT_i\exp(-i(k_{xi}x+k_{2,zi}(z-d))) \tag{B1-9}$$
$$H_{2,x}=-i\sqrt{\frac{1}{\mu_0}}\sum_i T_i\frac{-ik_{2,zi}}{k_0}\exp(-i(k_{xi}x+k_{2,zi}(z-d))) \tag{B1-10}$$
B2. 領域1-グレーティング領域の境界条件(z=0)を置く
B1-1からB1-8式から、領域1-グレーティング領域の境界条件を、z=0を代入して設定します。
z=0の両側で各\(k_{xi}\)成分が等しいとすると
$$ \delta_{i0}+R_{i}=\sum_{m=1}^{n} w_{i,m}(c^+_m+c^-_m\exp(-k_0q_md)\tag{B2-1}$$
$$ i(n_1\cos\theta\delta_{i0}-\frac{k_{1,zi}}{k_0}R_i)=\sum_{m=1}^n v_{i,m}(c^+_m-c^-_m\exp(-k_0q_md)) \tag{B2-2} $$
が得られます。
行列で表してみましょう。\(l=1,2\)に対して\( \mathbf{Y_1}=\text{diag}(k_{l,z1}/k_0, k_{l,z2}/k_0,\cdots) \)、\(\mathbf{c^\pm}=(c^\pm_1,c^\pm_2,\cdots)\)、\(\mathbf{X}=\text{diag}(\exp(-k_0q_1d),\exp(-k_0q_2d),\cdots)\)と置きます。diagはカッコの中身を対角成分とする対角行列です。
$$ \left(\matrix{ \delta_{i0} \cr in_1\cos\theta\delta_{i0}}\right)+\left(\matrix{\mathbf{I}\cr -i\mathbf{Y_1}}\right)\mathbf{R}=\left(\matrix{ \mathbf{W} & \mathbf{WX} \cr \mathbf{V} & \mathbf{-VX}}\right)\left(\matrix{\mathbf{c^+} \cr \mathbf{c^-}}\right) \tag{B2-3}$$
B3. グレーティング領域-領域2の境界条件(z=d)を置く
B2と同様にz=dでの境界条件を考えると、
$$ \sum_{m=1}^{n} w_{i,m}(c^+_m\exp(-k_0q_md)+c^-_m)=T_i\tag{B3-1}$$
$$ \sum_{m=1}^n v_{i,m}(c^+_m\exp(-k_0q_md)-c^-_m)=i\frac{k_{2,zi}}{k_0}T_i \tag{B3-2} $$
となり、行列にすると
$$\left(\matrix{ \mathbf{WX} & \mathbf{W} \cr \mathbf{VX} & \mathbf{-V}}\right)\left(\matrix{\mathbf{c^+} \cr \mathbf{c^-}}\right)=\left(\matrix{\mathbf{I} \cr i\mathbf{Y_2}}\right)\mathbf{T}\tag{B3-3} $$
B4. 行列をまとめる
B2-3, B3-3をまとめると次のようになります。
$$\left(\matrix{ \mathbf {I} & 0 &\mathbf{-W} & \mathbf{-WX} \cr -i\mathbf{Y_1} & 0 & \mathbf{-V} & \mathbf{VX} \cr 0 & \mathbf {I} & \mathbf{-WX} & \mathbf{-W} \cr 0 & i\mathbf{Y_2} & \mathbf{-VX} &\mathbf{V} } \right)\left(\matrix{\mathbf{R} \cr \mathbf{T} \cr \mathbf{c^+}\cr \mathbf{c^-}}\right)=\left(\matrix{-\delta_{i0} \cr -in_1\cos\theta\delta_{i0} \cr 0 \cr 0}\right) \tag{B4-1}$$
複雑になってきましたが、次のような形になります。
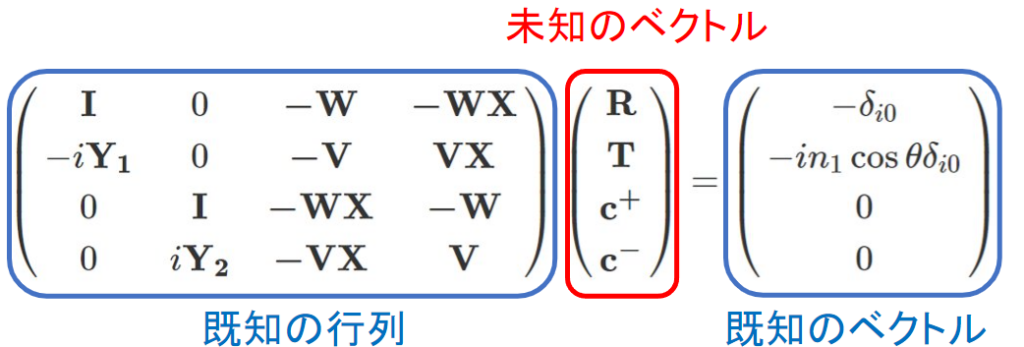
これは、左側の既知の行列の逆行列を作ることで、未知のベクトルの値を求められる式になります。
$$\left(\matrix{\mathbf{R} \cr \mathbf{T} \cr \mathbf{c^+}\cr \mathbf{c^-}}\right)=\left(\matrix{ \mathbf {I} & 0 &\mathbf{-W} & \mathbf{-WX} \cr -i\mathbf{Y_1} & 0 & \mathbf{-V} & \mathbf{VX} \cr 0 & \mathbf {I} & \mathbf{-WX} & \mathbf{-W} \cr 0 & i\mathbf{Y_2} & \mathbf{-VX} &\mathbf{V} } \right)^{-1}\left(\matrix{-\delta_{i0} \cr -in_1\cos\theta\delta_{i0} \cr 0 \cr 0}\right) \tag{B4-1}$$
これで、(数式的には)問題が解ける状態になりましたね。
B5.ポインティングベクトルの計算
回折効率の計算のために、平面波のポインティングベクトル\(\boldsymbol{S=E\times H}\)を計算します。電場・磁場を次のように複素数表示しているとすると、
$$ \boldsymbol{E}=\boldsymbol{E_0}(-i(\boldsymbol{k\cdot x}-\omega t))\tag{B5-1}$$
$$ \boldsymbol{H}=\boldsymbol{H_0}(-i(\boldsymbol{k\cdot x}-\omega t))\tag{B5-2}$$
ポインティングベクトルは実部を取る必要があるが、複素共役を用いて、ポインティングベクトルの時間平均は、
$$\bar{\boldsymbol{S}}=\frac{1}{2}\boldsymbol{E\times H^*} \tag{B5-3}$$
電場と磁場はマクスウェル方程式でつながっているので、TE波の場合、次のように電場\(\boldsymbol{E}\)に統一する:
$$ \bar{\boldsymbol{S}}=\frac{1}{2}\boldsymbol{E}\times (\frac{1}{-i\omega\mu_0}\nabla\times\boldsymbol{E})^*$$
$$=\frac{1}{2}\boldsymbol{E}\times (\frac{-i}{-i\omega\\mu_0}\boldsymbol{k\times E})^* $$
$$=\frac{1}{2\omega\mu_0}\boldsymbol{E_0}\times(\boldsymbol{k\times E_0^*}) $$
$$=\frac{1}{2\omega\mu_0}(\boldsymbol{k(E_0\cdot E_0^*)-E_0^*(E_0\cdot k)}) $$
$$=\frac{1}{2\omega\mu_0}\boldsymbol{k|E_0|^2} \tag{B5-4}$$
となります。
B6.回折効率の導出
各モードへの回折効率(反射:\(\eta_{ri}\), 透過側\(\eta_{ti}\))は、ポインティングベクトルのz成分の出射/入射比から求められます。
$$ \eta_{ri}=R_iR_i^*\text{Re}\left(\frac{k_{1,zi}}{k_0n_1\cos\theta}\right) \tag{B6-1}$$
$$ \eta_{ti}=T_iT_i^*\text{Re}\left(\frac{k_{2,zi}}{k_0n_1\cos\theta}\right) \tag{B6-2}$$
伝搬モードであるため、実部(Re)を取っています。
これで回折効率を求めることができました!
ちなみに… 回折効率には「絶対回折効率」と「相対回折効率」があります。絶対回折効率は、回折光強度と入射光強度の比で、相対回折効率は、(絶対回折効率)/(界面の反射率)のことです。要は、絶対回折効率は、トータルの効率、相対回折効率は、グレーティング形状で決まる部分の効率のことです。同じ形状でもコーティングによって絶対回折効率を上げることが可能ですが、相対回折効率は上げることができません。
参考:https://www.shimadzu.co.jp/products/opt/guide/03.html
B7 まとめ
今回は、前回引き続き、1次元RCWAでの効率計算方法の基礎をやってきました。式的に、解ける形になりましたが、数値計算上はまだ問題があります。解が安定するように、少し工夫する必要があるので、次回は実装上の問題を考えましょう。


コメント