【RCWA-4】1次元RCWAの基礎~行列計算の工夫~

前回は、RCWAの計算ができる見通しが立ちました。下の行列式を解ければ良いです。

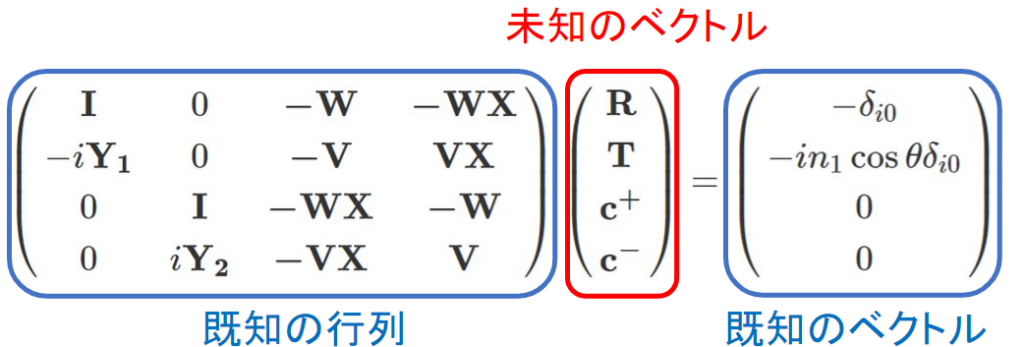
ただし、これだと行列式が大きすぎるので計算し辛いです。今回は計算しやすい形にするのがゴールです。

ちなみに各要素は次のとおりです。

$$\mathbf{Y_l}=\text{diag}(\{k_{l,zi}/k_0\}) \quad l=1,2$$

$$\mathbf{X}=\text{diag}(\{ \exp(-k_0q_id)\})$$

$$\mathbf{W}= \{\omega_{ij}\} ,\quad \mathbf{V=WQ},\quad \mathbf{Q}=\text{diag}(\{q_i\})$$

$$ \mathbf{c^\pm}=({c_i^\pm})$$

定義を忘れた場合は、前回記事・前々回記事を御覧ください.

C1. RとTを消去して、連立方程式を作る。
まとめ

C1. RとTを消去して、連立方程式を作る。

行列を合体させる前の式B2-3に戻ります。

$$ \left(\matrix{ \delta_{i0} \cr in_1\cos\theta\delta_{i0}}\right)+\left(\matrix{\mathbf{I}\cr -i\mathbf{Y_1}}\right)\mathbf{R}=\left(\matrix{ \mathbf{W} & \mathbf{WX} \cr \mathbf{V} & \mathbf{-VX}}\right)\left(\matrix{\mathbf{c^+} \cr \mathbf{c^-}}\right) \tag{C1-1}$$

この式は要は次の2式になります。

$$\mathbf{R=Wc^++WXc^–a_1} \tag{C1-2}$$

$$\mathbf{a_2}-i\mathbf{Y_1R}=\mathbf{Vc^+}-\mathbf{VXc^-} \tag{C1-3} $$

ここで、$\mathbf{a_1}\equiv \delta_{i0}, \mathbf{a_2}\equiv in_1\cos\theta\delta_{i0}$としました。すると、$\mathbf{R}$を消去できて、

$$(\mathbf{V}+i\mathbf{Y_1W)c^++(-VX}+i\mathbf{Y_1WX)c^-=a_2}+i\mathbf{Y_1a_1}\tag{C1-4}$$

同様に$\mathbf{T}$についても、式B3-3から考えましょう。

$$\left(\matrix{ \mathbf{WX} & \mathbf{W} \cr \mathbf{VX} & \mathbf{-V}}\right)\left(\matrix{\mathbf{c^+} \cr \mathbf{c^-}}\right)=\left(\matrix{\mathbf{I} \cr i\mathbf{Y_2}}\right)\mathbf{T}\tag{C1-5} $$

$\mathbf{R}$と同様に$\mathbf{T}$も消去して式を作ります(途中省略）。

$$(\mathbf{VX}-i\mathbf{Y_2WX)c^+}+(-\mathbf{V}-i\mathbf{Y_2W)c^-}=\mathbf{0}\tag{C1-6} $$

まとめて、行列の形にすると

$$\left(\matrix{\mathbf{V}+i\mathbf{Y_1W} & \mathbf{VX}+i\mathbf{Y_1WX} \cr \mathbf{VX}-i\mathbf{Y_2WX} & \mathbf{-V}-i\mathbf{Y_2W}} \right) \left(\matrix{\mathbf{c^+} \cr \mathbf{c^-}} \right)=\left(\matrix{\mathbf{a_2}+i\mathbf{Y_1a_1} \cr \mathbf{0}}\right) \tag{C1-7}$$

$\mathbf{c^\pm}$について解くと、

$$\left(\matrix{\mathbf{c^+} \cr \mathbf{c^-}} \right)=\left(\matrix{\mathbf{V}+i\mathbf{Y_1W} & \mathbf{VX}+i\mathbf{Y_1WX} \cr \mathbf{VX}-i\mathbf{Y_2WX} & \mathbf{-V}-i\mathbf{Y_2W}} \right)^{-1}\left(\matrix{\mathbf{a_2}+i\mathbf{Y_1a_1} \cr \mathbf{0}}\right) \tag{C1-8}$$

こちらは安定的に解けるようになっています。

$R,T$のほうが得たいパラメタなので、$\mathbf{c^\pm}$を消去して解こうとしたいですが、対角行列$X$はほぼゼロの行ができがちなので逆行列を安定して計算できないようです。

$\mathbf{c^\pm}$が計算できれば、$R,T$は元の式に代入して計算できます。

$$\mathbf{R=Wc^++WXc^- -a_1} \tag{C1-9}$$

$$\mathbf{T=WXc^++Wc^-}\tag{C1-10}$$