前回は、S4のwindowsへのインストールが完了しました。今回は簡単な計算をやってみます。S4は英語の記事しかほとんどないので、触りだけでも日本語の記事があるととっつきやすいのではないでしょうか。
状況設定
下のような状況を考えてみましょう。
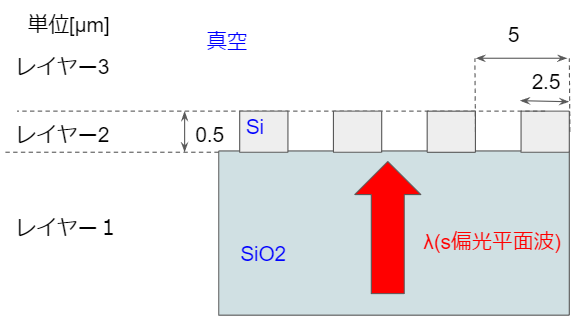
1次元のバイナリ回折格子です。サイズとかは今回適当に作ってます。(本当は狙いの波長が狙いの次数で最適になるように考えないと行けないですが、テストなのでいいでしょう)
コードを書いてみましょう。
import S4
import matplotlib.pyplot as plt
import numpy as np
import sys
#新しいシミュレーションオブジェクトを設定
S=S4.New(Lattice=((5.0,0),(0,0)),NumBasis=100)
#materialの設定
S.SetMaterial(Name='Vacuum',Epsilon=1)
S.SetMaterial(Name='SiO2',Epsilon=1.5)
S.SetMaterial(Name='Si',Epsilon=3.4)
#レイヤーを設定今回は3つのレイヤー。
S.AddLayer(Name='Substrate',Thickness=10.0, Material='SiO2')
S.AddLayer(Name='Level1',Thickness=0.5, Material='Vacuum')
#レベル1層にSi構造体を作ります。
S.SetRegionRectangle(Layer='Level1',Material='Si',Center=(0,0),Angle=0, Halfwidths=(1.25,0))
S.AddLayer('Air',Thickness=0,Material='Vacuum')
#波長範囲を設定
wavelength_array=np.linspace(0.501,2,100)
#効率計算結果用アレイ
efficiency_array=[]
for wavelength in wavelength_array:
S.SetFrequency(1/wavelength)
#入射角0度のs偏光平面波を入射する。
S.SetExcitationPlanewave(IncidenceAngles=(0,0),sAmplitude=1,pAmplitude=0)
#入射フラックスを取得
(P_incident,P_reflect)=S.GetPowerFlux(Layer='Substrate')
#各次数の透過フラックスを取得
P_transmittance=S.GetPowerFluxByOrder(Layer='Air')
#1次回折光の効率になおす。
efficiency=(P_transmittance[1][0]/P_incident).real
#アレイに追加。
efficiency_array.append(efficiency)
#進捗表示。
sys.stdout.write(f"\r wavelength={wavelength} eff={efficiency}")
sys.stdout.flush()
#matplotlibで表示
plt.grid()
plt.xlabel('wavelength [um]')
plt.ylabel('efficiency')
plt.plot(wavelength_array,efficiency_array)
plt.show()
これを実行すると、以下の結果が得られました。
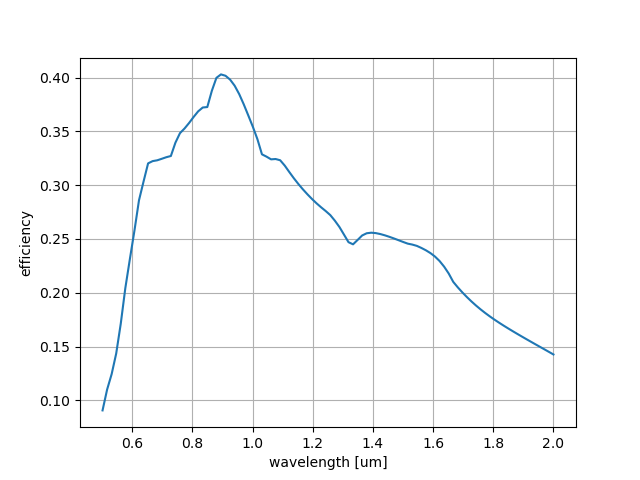
ちゃんと、適度な効率に収まっていますね。
計算パラメータを変えてみた
NumBasis=5に変えてみました。結果は下の図。
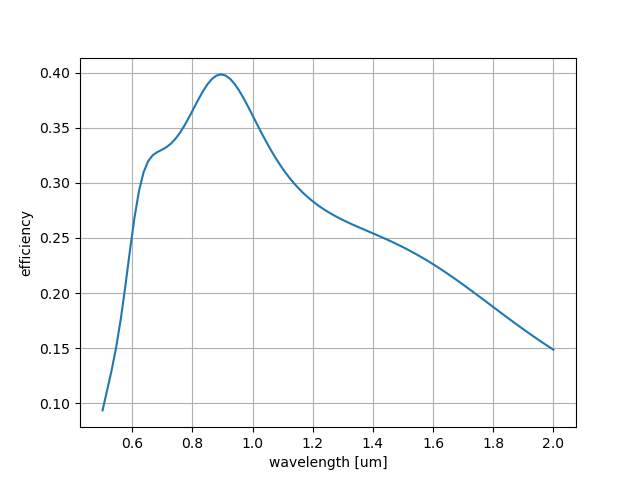
NumBasis=20の場合はこちら。
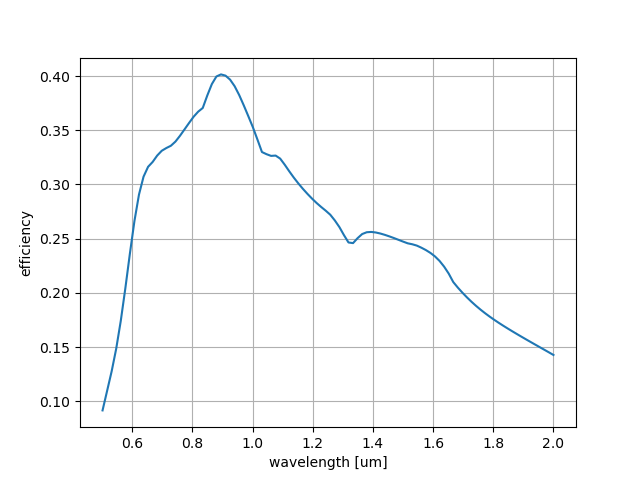
NumBasisが大きいほど、細かい特徴が現れています。
この「NumBasis」はフーリエ展開の最大次数を設定しています。なので、基本多めに設定しておくのが良いです。もちろん、次数が大きいほど計算コストがかかり、時間とメモリが食われます(私のマシンではNumBasis=500では動かなくなりました)
まとめ
とくにまとめることはないのですが、S4は非常に簡単にRCWA計算ができました。
層を設定して、構造を追加し、入射電磁波を与えて、何を出力するかを書いてやれば直ぐにできます。
また時間があれば、2次元計算とか、いろいろな機能を使ってみたいと思います。



コメント